peak deconvolution, peak fitting, overlapping peaks solving
(with Excel)

history, inside the problem, the software, how to use, examples, donations

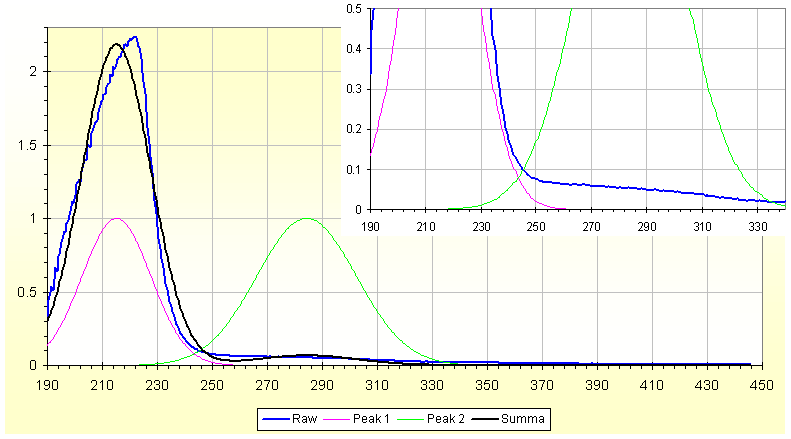
Fig.1, UV-Vis spectra, example of deconvolution of 2 overlap peaks, using this software

History

  Speaking about "peaks" is better use a common description, please read the following HPLC-GC troubleshooting before continue.

  With this small piece of software we do not like to solve all of previous problems, but only to find the 2 or 3 peaks able to produce a shape as in fig.1.

  One of the first applications of Chemometrics was the resolution of peaks overlap; today we have Parafac, Paralind, MCR and sometime PLS used for this. But this is too complex for my students as a first time approach.

  Also there are a lot of routine for Matlab/Octave or for "R" devoted to peaks deconvolution. But it is still difficult for my students to grasp all parameters used in those routine and often the subtended errors.

  Accounting all I said previously, I select Excel to deconvolute peak. It is not a new idea and you can be inspired reading the following:

1. From Prof. Thomas C. O'Haver, University of Maryland; some excel procedures for Spectral Deconvolution, please take a look,
2. Dr Roger M. Nix, Queen Mary, University of London; the develop of the famous eXPFit, a peak-fitting template for use with Microsoft Excel for the analysis of XPS and other spectral data (here eXPFit14 and eXPFit15 saved from oblivium),
3. From Dr. Stuart T. Gentry, LaSalle University; an Excel deconvolution and the instructions to use, (here Lab Oscillator Strengths Deconvolute saved from oblivium)
4. Inside the book of E. Joseph Billo (Excel for Scientists and Engineers, John Wiley & Sons, 2007) you can find a simple spreadsheet for spectra deconvolution. See the web pages of students Ruth Pontoriero with the spreadsheet,
5. From Dr. Leroy E. Laverman, UC Santa Barbara; instructions how to Curve Fitting with Solver.

Inside the Problem

  In the Fig.1 you can see the blue line, the raw data. The main peak probably ended at 250nm but another peak appears up to 370nm. This is a typical spectrum of water coming from the lake or river, using Suprasil cuvette with path length of 10mm.

  Is better to spent some time on the blue spectrum:

1. the main peak show a distortion, (some spectrophotometer could compress the data over 2.0 of absorbance), also the form of the peak is not symmetrical, lacking on the left parts (190nm is the limit of the instrument) and, finally, there is few noise "inside" the data,
2. of course the peak is not a Normal curve, nor a Lorentzian, nor a Cauchy curve, and probably not a Woldemar Voigt profile
3. but having probably only 2 peaks overlapped is better to have a Spectral Shape, see the examples in the link,
4. the second peak, probably at 290nm, is too small and we cannot describe it better. In this case the spectrometer is near the noise and near the LOQ. This is another problem that we have to focus on.

  Avoiding confusion we are doing a Curve Deconvolution, we found 2 or more peaks hidden under the Curve. Curve Fitting is a different mathematical work, finding a simple or complex equation able to describe the curve and able to minimize the distance among measured points and to obtaine the equation. To make a tentative of Deconvolution we must do more and more simplifications as:

1. the 2 curve must be simulated with an "easy to describe" distribution, as Gauss, Lorentz, Gosset, Cauchy, with formulae easy to be implemented in a spreadsheet, (and easy to be understand by undergraduate students),
2. assuming the cumulative spectra is only the mathematical sum of the 2 distributions,
3. assuming a linear correlation between raw data and the 2 simulated distributions (as in Multiple Linear Regression),
4. assuming the 2 hidden peaks to have the same shape and distribution type,
5. do not account possible fronting or tailing in one or more hidden peak,
6. for calculations find some variables to be optimized, design your Constraint on data, find a target,
7. use a form of iterative calculation, as Bootstrap, Montecarlo, Random walk, Brute force, or similar,
8. having and idea of possible centre values and width for the 2 subtended hidden peaks.

  For the point a) some researchers suggest the use of the Normal, Gaussian distribution as first step, and as an alternative the use of the Lorentz distribution (the type is linked with the detector of the instrument).

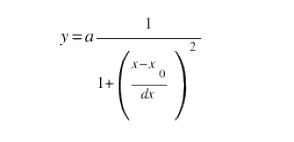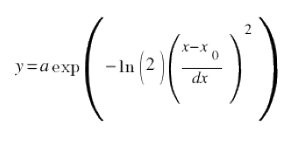Fig.2, on the left the Lorentz formula, the Gauss formula on the right. With: a=amplitude, dx=width HWHM, x0=maximum value

  For iterative calculation we can use Solver. Describe Solver is completely out of the scope of this page, if you are not a spreadsheet's wizard leave out this page immediately.

  Solver is available in Libre Office, Open Office and MS Office. Only to obtain compatibility we use Excel 2003 with standard Solver. There is a free GPL version of Solver named OpenSolver (it exists SolverStudio, free, but they use rather more commercial routines).

  If you like to know more on Solver use the links in this OpenSolver web page.

  To understand the calculation inside this software is better know something about LINEST function (see at Colby college, and on MS support), on the use of NORMDIST (on MS support, and on ExcelUser).

The Software

  This free software was distributed under Creative Commons Public License, CCPL 3.0, see my Copyright web page. Please read accurately the Liability Waiver in red.

  There are a few different versions, all work on MS-Excel 2000, up to MS-Excel 2003, some was tested on MS-Excel 2007 and 2010 version. All files are in .ZIP format to reduce size, available:

• deconvolution of 2 overlapped peak using Gauss distribution, 512 values for data set: GVisco_deconvoltution1.12_2Gauss.xls,
• as previous but with space for 1024 values in data set: GVisco_deconvoltution1.12_22Gauss.xls,
• deconvolution of 3 overlapped peak using Gauss distribution, 512 values for data set: GVisco_deconvoltution1.12_3Gauss.xls,
• as previous but with space for 1024 values in data set:: GVisco_deconvoltution1.12_33Gauss.xls,
• All of previuos, Gauss, in a single .ZIP file, please download, (719 KB)
• deconvolution of 2 overlapped peak using Cauchy-Lorentz distribution, 512 values for data set: GVisco_deconvoltution1.12_2Lorentz.xls,
• as previous but with space for 1024 values in data set:: GVisco_deconvoltution1.12_22Lorentz.xls,
• deconvolution of 3 overlapped peak using Cauchy-Lorentz distribution, 512 values for data set: GVisco_deconvoltution1.12_3Lorentz.xls,
• as previous but with space for 1024 values in data set:: GVisco_deconvoltution1.12_33Lorentz.xls,
• All of previuos, Lorentz, in a single .ZIP file, please download, (772 KB)
• the example for test the abcve software are in the file test data with spectra and chromatographic data (850 KB)

How To Use

  Dear students, this is not a course on Excel so you must already know how to use formulae and functions. I remember you to pass every lesson for Excel in this Course, please pass all lessons (and do ALL projects).

  To learn how to use is better download first the .ZIP file with some simulated curve (697 KB) and some real spectra.

  Very often the writer of a software is not the best writer of "instructions", he/she already know how to use! But I make here a tentative to describe how to use:

• download the simulated spectra/chromatograph and select one to start, best way is use the 2 Gauss curve from 100nm,
• download the Gauss curve version of the software,
• start MS-excel and load the simualted spectrum, open also the 512 values Gauss version,
• from 2-simulated-peaks.xls copy from A2 to B513 of "peaksumma" sheet, PasteSpecial/Values (or PasteSpecial/Text) in the GVisco_deconvoltution1.12_2Gauss.xls in the sheet "raw" pointing to A9,
• do not touch any other cells in the "raw" sheet and in the "calcu" sheet, pass to "view" sheet,
• you already have an idea on the center values of the 2 peaks (in this case about 300 and 600), and have an idea on the width of peaks (check with 80 and 100). If you not idea of aspected value, begin a chemist is not a good idea,
• fill with the previous values the cells from C8 to D9 in the "view" sheet,
• do not touch any other cells in the "view" sheet, (if you like you can change the min/max values of X axis to better show your graph)
• of course you already have installed and use Solver before, if not click Tools and click Solver, in the window click Options, on the new window clcik Cancel, returning to Solver window click Close (this is a method to fix/test some bad references in Excel module, but this is not an Excel lesson),

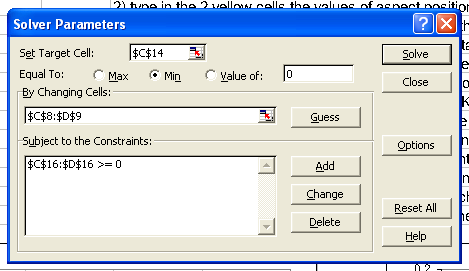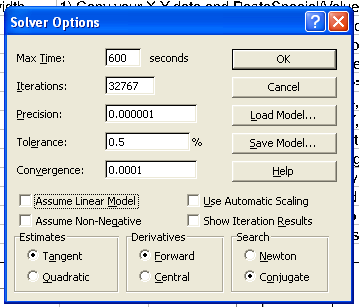Fig.3, the Solver parameter on the left with pointing cells, and the Solver options on the right

• in the Fig.3 the 2 windows of solver, please click on the Options and do a setting similar to the show in the right. Close the Options with OK and check if the pointing cells are the same of the left part of Fig.3,
• if you are follow all of previous instructions and don't touch any other cells the celle references in Solver Parameters are already correct,
• click on Solve and wait some seconds, probably a windows similar to Fig.4 appears,

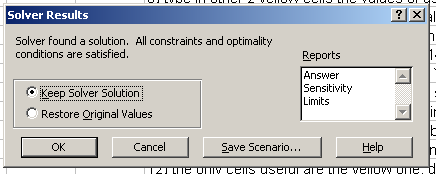Fig.4, the Solver results, click only on OK to accept

• the Fig.4 show the results, really show a some option, for us none is interesting, if Keep Solver Solutions is selected click only on OK,
• teh solver close itslef and you can find the center values of the peaks in C8, D8, also in C17, D17 are show the errors of the modelling, and in C18, D18 the estimated height of the peaks,
• some other resuslts are show as r² useful to describe the model.

  Having a result is better change a little the starting values (from C8 to D9). Write in a paper the results, change C8..D9 and restart Solver, write results.

  Do it for 3 or 5 times and probably obtain a better model, The starting point are very important, more in 3 peaks deconvolutions.

Examples

  The simple example is in the file 2-simulated-peaks.XLS with a simulated spectra with peaks at 300nm and 600nm. Can be solved with 2 Gauss method. Be careful, must be enlarged the space for dataset in the main .xls file, from 512 to 574 values.

  One other example is in the water-spectra.xls file. It is an hard work, the 'human' see the second peaks, probably broad, at about 270 nm, but can the model find it?
  As previous stated the main peak is heavy distorted by instrument saturation so find the first solution is difficult also. One other problem is the left side of the main peak, missing!
  Please open the GVisco_deconvoltution1.12_2Gauss.xls file, open also the water-spectra.xls file. Copy the 2 columns from water-spectra and PasteSpecial/Text in the "raw" sheet.
  To first step I suggest the values of 220 and 270 for posistion and 10, 20 for width. Run Solver with previous show parameters.

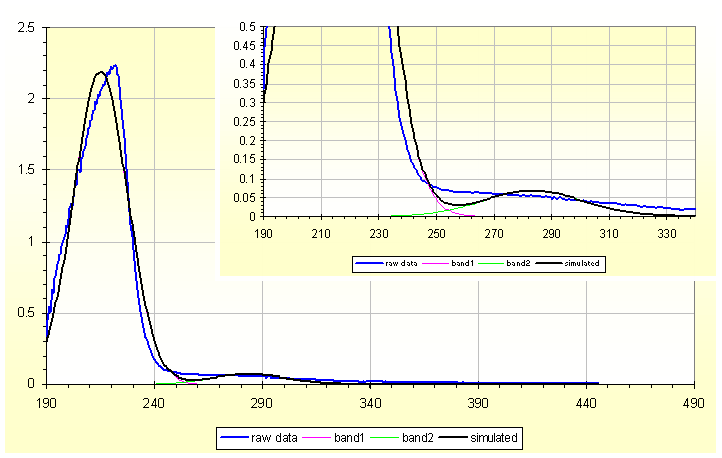Fig.5, a Gauss solution for water-spectra.xls, with 215 and 284 nm

  One other possible solution is 215, 281 for position and 2.184, 0.068 for height. But find other yourself.

  There are other excel files as example, one is the file IC-chromatog.XLS inside very interesting are the sheet "brwash2or" with 2 peaks at, about, 177sec and 210sec. In the same file there is the sheet "wash_pulp" with 3 peaks at about 176, 188, 199 seconds.

  One other example is in the file chm-150.XLS, it come from a laboratory excercise of Prof. James B. Foresman with title "CHM 150: Computers in Chemistry Seminar". This example is more complex, you must first remove the negative values on baseline (probably with the use of our software on scaling) and after define the 2 probably vaules of nanometers for the peaks on the left of the spectra.

Tips

  If you know Excel you can expand or reduce the 512 rows, and probably can desing a solution for 4 peaks, but this one other history.

Donations if you have a Bitcoin wallet

  If you have a nice fat wallet you can send a few cents to this code 1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6 maybe with a message (be careful to the transaction cost, send 0.1 and pay 0.01 is not a good idea).

1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6    <== my code , Thank you.

Donations if you have not a Bitcoin wallet

  If you like this work and measures you can make a small donation of Bitcoin. You do not need a wallet to make a donation, indeed even those who have Bitcoin wallet is better to pass for a web site that "gift" currency since this does not have a transaction cost.

  To make a donation you must use some of your web-time. Go to www.GreenBitCo.in, enter my code 1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6 enter the Captcha code that you see, press "Claim Now" button. Wait 15 minutes on the publicity page, when the 15 minutes pass fill the new Captcha and press "Claim Now" again. To get some value are necessary 10 pages or more. Be careful, do not use roulette, dices, casino and other stealing web site.

1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6    <== my code , Thank you.

     

Back Page   read help   C^© Copyright   we did it