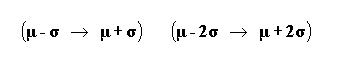
| Rome University, La Sapienza Chemistry Department Rome, Italy, Europe |
Dr. Giovanni Visco, April 2003 Cenni di statistica. Distribuzioni, Gauss, Student, Beta, ... Parametri: media, mediana, moda, percentili, kurtosi, outlier, ... |
Corso di Laurea in: Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione Corso di laurea in: Chimica Ambientale |
| previous slide, 24 | all lessons, these slides index | next slide, 26 |
Per semplicita' definiamo questo termine per la sola distribuzione Normale o di Gauss. Una volta definita la media aritmetica e calcolato lo scarto quadratico medio si possono calcolare i valori
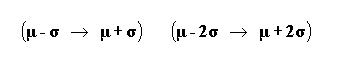
Che si possono far corrispondere con facilita' al grafico della distribuzione Normale (disegnato con il file gia' visto). Per semplicita' e' stata scelta la distribuzione con media=0 e s.q.m.=1. L'area colorata racchiude tutti i punti della distribuzione che giacciono fra -s.q.m. et + s.q.m., cioe' la formula qui sopra a sinistra.
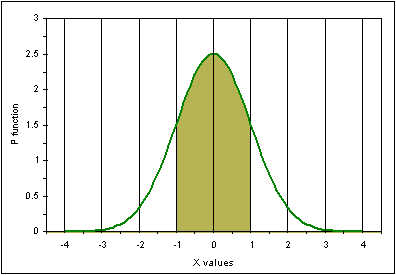
Ci dice [confidence interval] che nell'area colorata abbiamo confidenza di trovare il 68.27% dei dati. Cioe' al variare della distanza dalla media, usando come parametro di distanza lo s.q.m. possiamo conoscere, probabilisticamente, quanti valori della distribuzione ricadono all'interno dell'area definita.
| distanza dalla media in +/- s.q.m. (e valore di Zα) | 0.6745 | 1 | 1.28 | 1.645 | 1.96 | 2 | 2.05 | 2.33 | 2.58 | 3 |
| Gauss, valore in % di dati raccolti sotto la curva | 50 | 68.27 | 80 | 90 | 95 | 95.45 | 96 | 98 | 99 | 99.73 | α = | 0.5 | 0.3173 | 0.2 | 0.1 | 0.05 | 0.0455 | 0.04 | 0.02 | 0.01 | 0.0027 |
Per dirla ancora diversamente: se raccogliamo tutti i dati compresi fra media-2s.q.m. et media+2s.q.m. (la formula a destra qui sopra) abbiamo una probabilita' del 95.45% che i dati siano in questo intervallo. A proposito di α, ci servira' nel test delle ipotesi, nel test di Student, etc.
| previous slide, 24 | all lessons, these slides index | next slide, 26 |