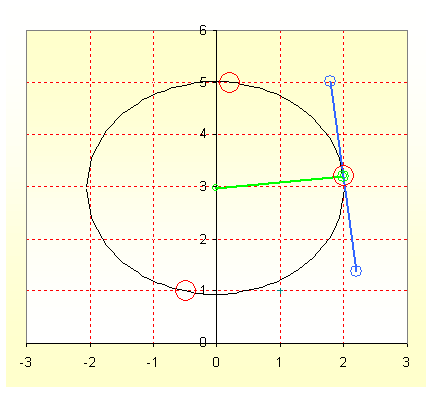
the radius and in blue the tangent, pass the mouse for example
 |
| Fig.1, the example of a conical passing among 3 points, in green the radius and in blue the tangent, pass the mouse for example |
The exact definition is differentiation. Probably the first calculus of differentiation is stated in 1600 from Isaac Newton or Gottfried Wilhelm Leibniz, the paternity is disputed.
The first derivative is used in chemistry to find the inflection point in a curve (the example of Fig. 1 is the measure of Carbonate and Hydrogen Carbonate in a water), to find the flex point or peaks. The derivative is not only used in chemistry, every branch of science needs it.
Of course there are more for Matlab/Octave and for "R" devoted to solve this problem. But it is still difficult for my students to grasp all parameters used in those routines and often the subtended errors.
Accounting of all I said previously, I have selected Excel to better calculate the derivative. Yes, Excel another time, see the software section.
From instruments, from data acquisition, from an experiment we always obtain a large or small number of points, often X-Y, or so called a "discrete distribution". Probably is possible to calculate a polynomial function able to fit our X-Y series, but it is way impractical on many software, start from the discrete distribution to calculate the derivative.
In the Fig.2 you can see part of a chromatogram with an evident peak, but see also the quantisation of the data. And this is another problem, read below.
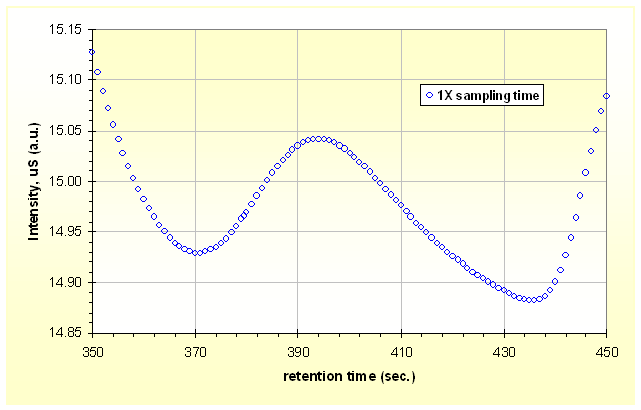 |
| Fig.2a, a typical chromatogram with discrete sampling. Fig.2b with higher sampling frequency |
More and more (simple) software use the difference between 2 consecutive points (or ΔY/ΔX) to compute derivative. But if we see the Fig.2b it is better to describe the peak having a 2x sampling time. Nevertheless, the differences between 2 consecutive points are smaller when we use a greater scanning speed.
In other words, it is difficult to calculate the derivative, or derivative values are smaller and useless.
The idea is to compute "a conical" around the point where we want to compute the derivative. 2 possible conicals are the circle and the parabola and probably we can use the ellipse as well.
For this version of the software, we use the circle computed with 3 points around the point where we want the derivative, next time we will work on ellipse and parabola.
This free software was distributed under Creative Commons Public License, CCPL 3.0, see my Copyright web page. Please read accurately the Liability Waiver in red.
There are only two versions working on MS-Excel 2000, up to MS-Excel 2003, was tested on MS-Excel 2007 and 2010 version. Are available:
Probably is clear reading the filename, but the 2 version of the software use the same algorithm and computation, but one of them use the point 2,3,4 after the points 3,4,5 and after the points 4,5,6 to calculate the derivative of point 3 or 4 or 5. The alternative version is use the point 1,3,5 after the points 2,4,6 and after the points 3,5,7 to calculate the derivative of point 3 or 4 or 5.
The 2 versions produce a completely different derivative (in some cases), the 1-3-5 is unsuggested but can be use to solve strange problems with noise or oversampling.
The software accepts only X values, and consequently the Y values, monotone, rising of downing. The software resists to two X with same values (or two Y in other zone).
For computation of conical we use extensively the determinants, 4 in every point, and for some dataset one of them cannot converge and you surely obtain an error, check our Tips & Tricks section.
Dear students, this is not a course on Excel, so you should already know how to use formulae and functions. I remember you to pass every lesson for Excel 2003 in this Course, and after that, pass all lessons of 2010 version (and do ALL projects).
Very often the writer of the software is not the best writer of "instructions", he/she already knows how to use it! Nevertheless, I have made here a tentative to describe how proceed:
There are 6 examples in the file GVisco_3points-conical-derivative-examples.xls. The first is the example already present in the software, another example similar but it shows a poor dataset. The third is chromatographic peak and the fourth the same peak but in downsampling.
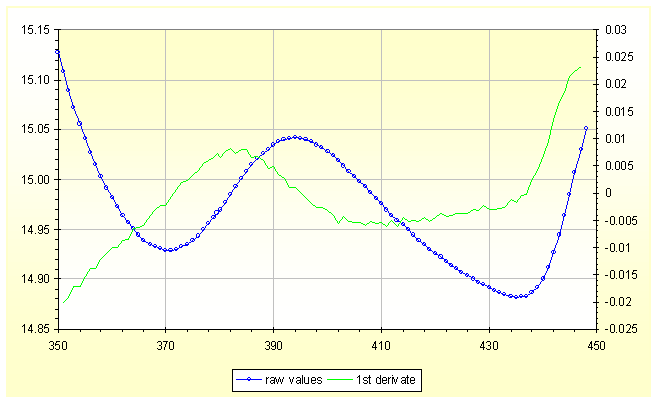 |
| Fig.3, the solution for the peak of fig.2a. The green line needs an interpretation. |
Interesting are the 2 derivatives obtained from example 3 and from example 4. It is shown in Fig.3 and a young chemist can be asked for an interpretation in an exam on instrumental analysis!
Tips & Tricks
The following data come from a work on reflectance of stones measured to check the "cleaning". In some cases, one of the determinants do not converge, so we obtain the error in reds in table below.
| wavelength (nm) | 570 | 580 | 590 | 600 | 610 | 620 | 630 | 640 | 650 | 660 | 670 | 680 |
| reflectance (%) | 56.40 | 56.33 | 56.36 | 56.21 | 56.06 | 55.95 | 55.61 | 55.60 | 55.42 | 55.24 | 55.12 | 54.95 |
| ok or change? | ok | ok | ok | change | ok | ok | ok | ok | change | ok | ok | ok |
| 1st derivative | +0.0245 | -0.0120 | +0.0120 | #DIV/0! | -0.0170 | +0.0005 | -0.0505 | +0.0075 | #DIV/0! | -0.0210 | -0.0095 | -0.0220 |
| new reflect. (%) | 56.40 | 56.33 | 56.36 | 56.22 | 56.06 | 55.95 | 55.61 | 55.60 | 55.43 | 55.24 | 55.12 | 54.95 |
| 1st derivative | +0.0245 | -0.0120 | +0.0115 | -0.0130 | -0.0185 | +0.0005 | -0.0505 | +0.0070 | -0.0160 | -0.0225 | -0.0095 | -0.0220 |
To solve it, first make a chart and see the X-Y curve, reading the curve you can find if it adds or subtracts a small value to Y. We suggest changing the Y value from 0.1% up to 1%, not more.
As example, in table, the value 56.21 becomes 56.22 and the value 55.42 become 55.43, and ............. the determinant converge! Se also the values in green, also the numbers in 1st derivative around the error change a little.
The software is designed for 100 or 256 values and the space can be enlarged or reduced. But in this case, having 4 determinants, and using a not linear placement of the datapoints, it doesn't so easy expand or reduce the working matrix of 100 or 256 data points. You need almost medium competences on Excel to do it.
Donations if you have a Bitcoin wallet
If you have a nice fat wallet you can send a few cents to this code 1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6 maybe with a message (be careful to the transaction cost, send 0.1 and pay 0.01 is not a good idea).
1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6 <== my code , Thank you.
Donations if you have not a Bitcoin wallet
If you like this work and measures you can make a small donation of Bitcoin. You do not need a wallet to make a donation, indeed even those who have Bitcoin wallet is better to pass for a web site that "gift" currency since this does not have a transaction cost.
To make a donation you must use some of your web-time. Go to www.GreenBitCo.in, enter my code 1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6 enter the Captcha code that you see, press "Claim Now" button. Wait 15 minutes on the publicity page, when the 15 minutes pass fill the new Captcha and press "Claim Now" again. To get some value are necessary 10 pages or more. Be careful, do not use roulette, dices, casino and other stealing web site.
1ETv1mJTZTB7EiXwZkucF2BTA512Rkaw6 <== my code , Thank you.
| Universita' Degli Studi di Roma La Sapienza |
Dr. G. Visco appointed professor for chemometrics & .... |
Corso di Laurea in: Scienze Applicate ai Beni Culturali ed alla Diagnostica per la loro Conservazione |